浙江省考复习干货！资料分析之速算技巧+公式合集

　　资料分析在行测中属于性价比较高的一类题型，若是能沉下心来攻克此类题型，很容易拉开跟其他考生的差距。

　　但大家做资料分析总会存在一些问题，如材料难读、做题顺序不对、数据找错、年份看错、数字大，计算难等，本文梳理了5个非常实用的速算技巧，希望能帮助大家提高做题速度。

　　一、巧用分数（适用于乘除法）

　　应用场景：若所列式子中有某个数可以近似的转化为一个常见分数，我们可以将其化为分数进行计算。

　　这里要申明的一点是，这个方法的运用需要先记住一些常用的分数对应关系：

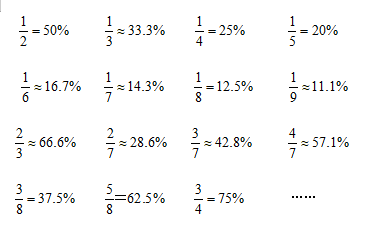
　　【建议收藏或摘抄这组数据，把它设置成屏保或者聊天背景，不时加强记忆，不要怕麻烦，记忆这组数据远不及你在考场抓耳挠腮来的痛苦】

　　大家可以先尝试用自己的方法计算以下计算题组，记得开刷前开始计时，看看做完自己用时多久~

　　262×50=

　　286×333=

　　111×825=

　　如果用平常的方法去算的话，1分钟之内是很难完成这些计算的，但是如果巧用分数的话，30秒即可就从选项中定位正确答案~不信你看??

　　50→1/2     262×50=262÷2×100=13100

　　333→1/3   286×333≈286÷3×1000≈95300  （准确答案为95238）

　　111→1/9   111×825≈825÷9×1000≈91600   （准确答案为91575）

　　PS：这里可能会有同学纠结小数点，其实大可不必，因为题目都是选择题，你只需要去匹配数字，做到胆大心细即可。下面我们用两道例题佐证一下：

　　【例题1】2015年1-7月，我国机电产品出口额44359.4元，同比增长1.2%，占出口总额的57.2%。问：2015年1-7月，我国出口总额为（ ）。

　　A.63534.0元

　　B.77551.4元

　　C.82907.1元

　　D.95772.7元

　　【解析】相信大家之前都做过这道题，都动笔了吧？其实这道题直接口算即可，我给大家详细讲一下思路：

　　列式子：44359.4÷57.2%

　　联想：57.2≈57.1约等于4/7

　　则有：44358÷4×7

　　如果你观察了选项的话，此时只计算前两位44÷4×7=77已经可以得出正确答案了。

　　【例题2】依然为行测罗盘中的一道题

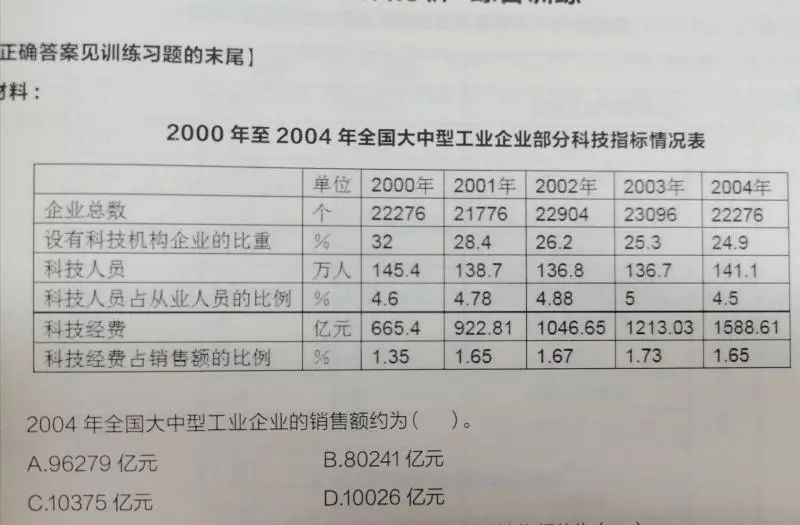
　　【解析】

　　根据题目列式子：1588.61÷1.65%

　　1.65%近似于1.67%，我们可以联想到16.7%≈1/6

　　那么是不是可以这样？1588.61÷1.65%=1588.61÷（1/6）=1588.61×6

　　算到前两位观察选项已经可以知道答案为9XXXX了，秒选A。

　　（注：大部分时候不用纠结1.65%和16.7%的×10的换算，因为观察选项能算出首位数字就能选出答案了，所以大家一定要注意观察选项~）

　　对比前面这几组数据的正确答案可以看到，巧用分数计算出的答案已经比较精确，算出前几位数字足以让你选出正确答案。最后再次跟大家强调，熟练运用这个方法的前提是熟记常用的一些分数转化，唯有厚积才能薄发。

　　巧用分数法就和大家说到这儿，对于计算如此复杂的资料分析来说，这个方法肯定是不够用的，接下来我们再看看另一个方法——拆分法。

　　二、拆分法

　　不同于巧用分数法，这次我们聚焦于百分数，依然乘除法都可以适用：

　　（1）除法的拆分

　　应用场景：

　　一：如果分数大小接近1(分子分母相差不大)，可用100%减去；

　　二：如果分子在分母的50%附近，先拆出50%；

　　三：如果分子很小，可根据实际情况拆出10%或5%或1%；

　　看着是不是有点懵？

　　没关系，我们直接用一两道真题来感受一下：

　　【例题3】：全国2007年认定登记的技术合同共计220868项，同比增长7%；总成交金额2226亿元，同比增长22.44%；平均每项技术合同成交金额突破百万元大关，达到100.78万元。

　　技术秘密和计算机软件著作权的技术交易成交额居第一、二位，技术秘密合同成交76261项，成交金额1008亿元，较上年增长29.2%；计算机软件著作权合同成交27617项，成交金额255亿元，较上年增长了15.4%。

　　问：2006年技术秘密合同成交金额占全国技术合同总成交金额的比重是多少：

　　A.42.9%       B.45.3%       C. 65.2%         D. 68. 2%

　　【解析】根据题目可知，求的是前期比重，公式为：

　　如果是我的话其实算到第一个分数为45%已经可以选出正确答案A了，为什么呢？注意观察选项朋友们，122/129明显小于1，两数相乘得到的肯定稍小于45%，看选项只有A符合条件。

　　当然如果你不放心非要再算一步的话也行，94%×45%的计算可以用到我们乘法的拆分：94%×45%=94%×（50%-5%）=47%-4.7%=42.3%，选A。（关于乘法拆分下面还有详细说明）

　　此方法大家还可用下面一组数据练一练：

　　685/752   （100%附近）

　　265/522   （50%附近）

　　456/898   （50%附近）

　　225/632   （1/3;33.3%附近）

　　在这里我就只给大家详细的演算第一个式子，其余的大家可以自己练一练。

　　（2）乘法的拆分

　　应用场景：若乘法中有某个乘数为百分数且能拆成两个简单数值(50%、10%、5%等)，我们可以将该百分数拆成两部分再相乘。

　　常用的小数拆分有：

　　45%=50%一5%；55%=50%+5%；15%=10%+5%；

　　60%=50%+10%；95%=1一5%；90%=1一10%……

　　【例题4】:某地区2014年的地区生产总值为1500亿元，第一产业生产值占地区生产总值的17.8%,问该地区2014年的第一产业生产总值是多少?

　　【解析】:列式子：1500×17.8%，我们如何把17.8%进行拆分才好算呢？

　　观察得17.8%=20%-2%-0.2%

　　则有：1500×(20%-2%-0.2%)，

　　这样整个式子就非常好算了，不就是300-30-3=267么。

　　最后再提供几个式子大家算一算找找感觉：

　　478 × 15%=

　　687X60% =

　　1456 X 55%=

　　以上两种方法都是针对乘除法的，接下来我们再来看看首、尾数法。

　　三、首、尾数法

　　首、尾数法主要适用于求解多个数的和/差，且选项的首/尾数各不相同时，可以使用该方法快速选出正确选项。

　　举个例子具体运用一下：

　　【例题5】

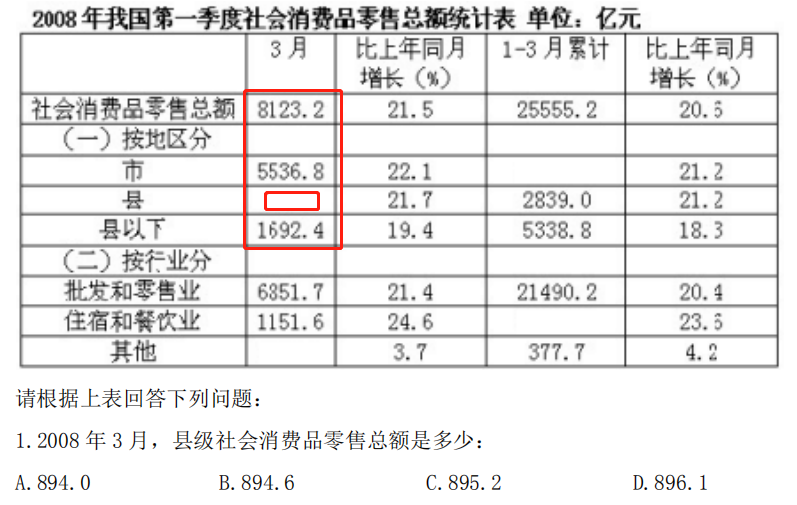
　　【解析】此题先观察选项，首数相同、尾数不同，用尾数法，有：8+4+X=#2；所以，所求数据的尾数应为0，秒选A。（注：精确求差同样适用）

　　首、尾数法相对而言比较简单，这里不再过多的进行说明。

　　到这儿三个方法都已经介绍完了，相信认真看了的小伙伴会注意到有一个步骤频繁出现，那就是——观察选项。

　　观察选项是做资料分析时很好的一个技巧点。因为有的题目其实只要算一两步就可以选出正确答案了，没必要算出一个完整的数值浪费多余的时间。

　　例如下面这道题：

　　【例题6】2012年全国公路水路交通固定资产投资14512亿元，占全社会固定资产投资的3.9%。分地区看，西部地区交通固定资产投资5400亿元，所占比重为37.2%，比上年提高1.2个百分点；东、中部地区交通固定资产投资分别为5479亿元、3633亿元，所占比重分别为37.8%和25.0%。

　　问：2012年全社会固定资产投资约为多少万亿元?

　　A.45.33

　　B.40.14

　　C.42.58

　　D.37.21

　　【解析】：

　　根据“全社会固定资产投资”迅速定位首句，

　　分析问题列式：14512/3.9%=3XXXXX，

　　观察选项秒选D。

　　四、分数大小比较

　　你能快速比较出下面2组式子之间的大小吗？

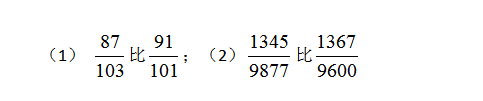
　　相信部分考生观察式子过后，无需计算或简单口算就能快速秒杀，得出结论。不过，如果你还在动笔算，咳咳，去反思一会儿吧。

　　没错，上面用到的就是分数的一个特性：

　　当我们在进行比较的时候，发现两个分数中一个分子比对方大，分母比对方小，则分数一定会比对方大。

　　例如：9/5一定大于8/6

　　这两组式子都是第二个分数的分子小（101<103，9600<9877），分母大(91>87，1367>13445)，则分数也较大。这是分数比较中较为简单的一种情况，碰到了也是出题老师仁慈了。

　　在做资料分析时我们经常会碰到增量大小比较或者增长趋势（比重、比值等）比较，而所给的数据通常都很复杂，比如像下面这样的式子，你还能快速得出结论吗？

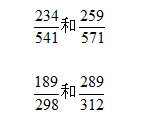
　　我来向大家介绍一下两个分数比较大小的判断规律：

　　1、分子增速大于分母，则分数变大（比重上升）

　　2、分子增速小于分母，则分数变小（比重下降）

　　3、分子增速等于分母，则分数不变（比重不变）

　　何为分子/分母的增速呢？

　　拿上面的两组数来看，分子：234到259，增长了25，增速为25/259

　　分母：541到571，增长了30，增速为30/541。

　　然后再比较两个增速大小，25/259≈1/10，30/541＜1/10，So对于第一组数来说，分子的增速大于分母， 则：

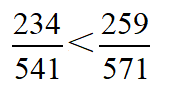
　　这样是不是只要在试卷上简单的算一下加减法就行了？大家可以再试着算一算第二组数，答案评论区见~下面我们看一道例题：

　　此题求的是增长率的大小，，根据公式，可以得到以下四个式子：

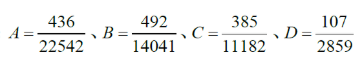
　　我们可以先观察一番，看看有没有选项可以直接心算排除，B选项和A选项相比，分子大，分母小，所以B＞A，先直接排除B选项；

　　再看C和A，385-436，增长了近1/3，11182—22542增长了近100%，所以分子增速小于分母，分数变小C＞A，排除C选项。

　　再看D选项，这个就更好算了，明显D到A，分子增速要小于分母，分数变小，所以A＜D。

　　这道题答案选A。

　　这道题是直接比较增长率的，下面我们再来看看另一道例题：

　　这道题数据很多很乱，大家在找数据时一定要仔细！！要静下心来捋清楚。下面回答正题，来看看这道题怎么解。

　　总的来说，题目需要算三个数据，全国第一、二、三产业城镇固定资产投资增长率分别为分母，同期江苏第一、二、三产业城镇固定资产投资增长率分别为分子。如下图所示：

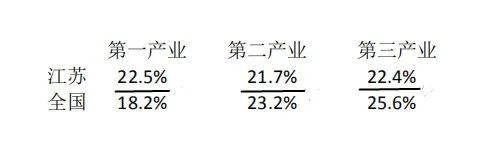
　　由此，根据之前提到的判断规律，可以看出第一产业的比重上升，第二、三产业下降，答案选A。

　　五、中间值法

　　中间值法适用于当你对答案有了一个估算的值，但无法确定二选一该选哪一个，且这两个选项分布在一个比较规整的数两侧，此时可以考虑使用插值法。

　　比如你列式子得出来一个值为541/675，估算答案大概在80%左右，排除后剩下的两个选项分别是79.8%和80.1%。

　　此时我们就可以用675×80%大概估一下，看得出来的数和541比谁大谁小。

　　如果大了，说明675应该乘以一个小于80%的数才能得到541，此时答案应该选79.8%。

　　如果小了，说明675应该乘以一个大于80%的数才能得到541，此时答案可以选80.1%。

　　在进入下面的例题讲解之前大家再一下这张表：

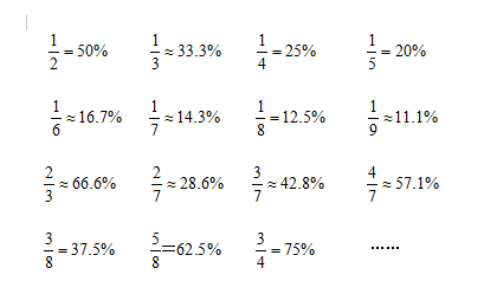
　　下面我们来看一个例题，

　　2006年，某厂产值为13057.2万元。2007年，增产3281.3万元，2007年该厂产值增值率为（ ）。

　　A.25.13%   B.24.87%   C.31.18%   D.18.96%

　　根据题干列出算式:

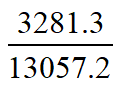
　　大家可以先根据3/13大概估算一下在1/4左右，也就是25%左右，可以排除CD选项。

　　由于AB太接近了，若是直接算肯定这个性价比是不高的。若是直接省掉算式的后三位，算32/130,得出的是24.6%，你肯定会选B，然而，正确答案是A，这个时候到底该怎么算才简单呢？

　　我们不妨取两个选项的中间值25%，即直接用13057.2×25%，有同学会疑惑，明明这看着也很难算啊！别急，往下再看看：

　　25%=1/4，13057.2×25%=13057.2×（1/4）=13057.2÷4=326…   这是不是就很容易算了？

　　326＜328，所以正确答案应该比25%大一点，选A。

　　下面我们再用一道例题来实战一下。

　　2006年，全国农村从业人员数量为47852万人，其中6986万人从事第三产业;东北地区农村从业人员数量为3230万人，其中391万人从事第三产业。请问，全国、东北地区农村从业人员中从事第三产业人员的比例分别是多少?( )

　　A.13.6%，12.7%

　　B.14.6%，12.7%

　　C.13.6%，12.1%

　　D.14.6%，12.1%

　　根据题干信息，可列出两个等式：

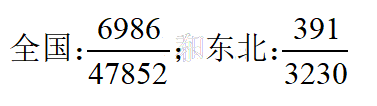
　　观察选项可知，6986/47852，结果要么是13.6%，要么是14.6%，二者之间有个14.3%，即1/7，所以我们先看看47852的1/7是多少，47852/7明显小于7000，但是6986极其接近7000，所以6986/47852肯定大于14.3%，故全国的比例应为14.6%。

　　东北地区农村：391/3230，结果要么是12.7%，要么是12.1%，二者之间有个12.5%，即1/8，所以我们先看看3230的1/8是多少，明显超过400，所以391/3230比12.5%小，所以只能是12.1%。

　　试问如果你辛辛苦苦的算完去看选项发现只有D答案的首位是3，心情该是多么的“美妙”？所以大家要有意识的去培养这个习惯，不需要花很多时间，你只要瞄一眼留个大概的印象就行。

　　六、资料分析必备公式

　　增长的常考考法

　　间隔增长率

　　
　　混合增长率

　　混合增长率 - 十字交叉法

　　等速增长

　　比重的常见考法

　　两期平均数的比较

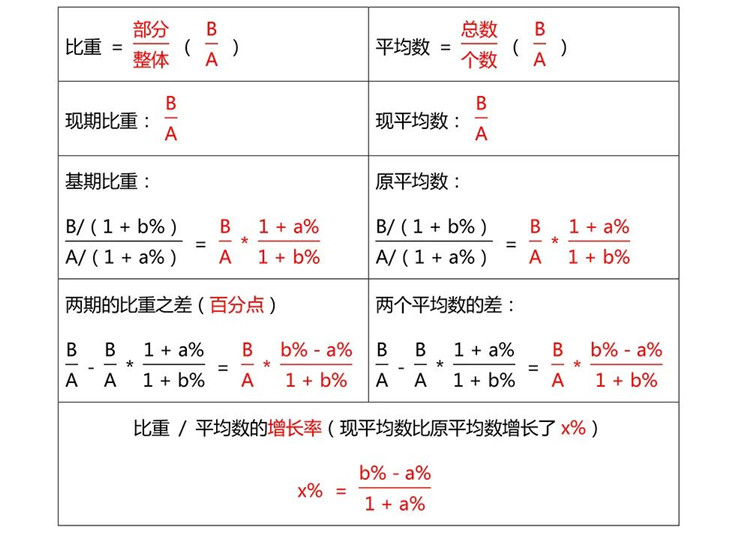
　　通过以上例题、技巧梳理及公式罗列，是不是对资料分析这一模块的重要考点有了更深刻的认识与掌握呢，记得抽空花点时间去把该掌握的方法技巧及速算公式去理解熟记，当然刷题去灵活运用肯定是少不了的。